2.2 Lösungen
Die Quelltexte der Lösungen stehen auch im Paket de.hsbo.fbv.bmg.vectors.aufgaben zum Download bereit.
Aufgabe 1:
| a | b | ∠(a,b) | a⋅b | a×b | b×a |
|---|---|---|---|---|---|
| (1,0) | (0,1) | 90° | 1 | -1 | |
| (3,0) | (0,4) | 90° | 12 | -12 | |
| (3√(½),3√(½)) | (0,4) | 45° | 12√(½) | 12√(½) | -12√(½) |
| (3√(½),3√(½)) | (4√(½),-4√(½)) | -90° | -12 | 12 |
Aufgabe 2:
Vector
Datum: 2.11.2011 Größe: 4.8 KB
Aufgabe 3:
Coordinate
Datum: 2.11.2011 Größe: 2.1 KB
Aufgabe 4:
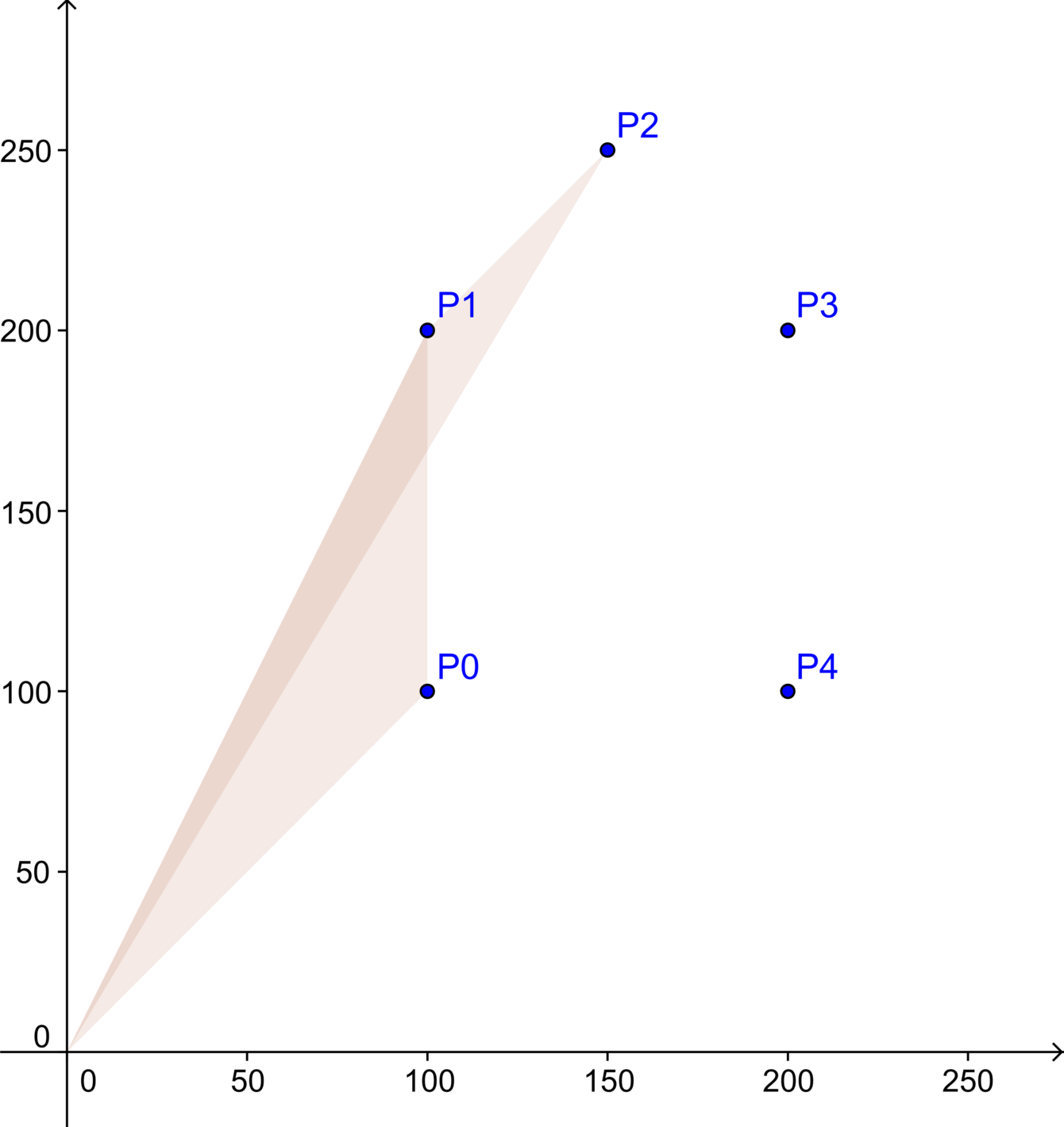
Prinzip der Flächenberechnung:
- Gesuchte Fläche wird in Dreiecke zerlegt.
- Der Flächeninhalt eines Dreiecks ist halber Flächeninhalt, der durch das Kreuzprodukt entsteht.
- Da das Kreuzprodukt gerichtete Flächen zurückgibt, heben sich die überlagernden Flächen (im Bild dunkel) in der Summe auf.
Umlaufrichtung der Stützpunkte:
- Ist der Flächeninhalt positiv, dann wurden die Punkte im mathematischen Drehsinn besucht (Rechte-Hand-Regel).
- Ist der Flächeninhalt negativ, wurden die Punkte im Uhrzeigersinn besucht.
Aufgabe 6:
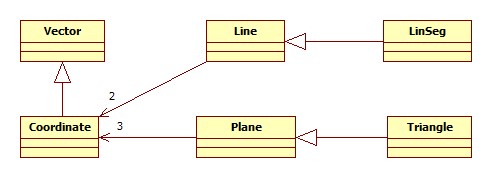
Die Klasse Line (für Geraden) sollte folgende Elemente enthalten:
- Zwei Attribute c0 und c1 vom Typ Coordinate, die die Lage und Richtung der Geraden festlegen. Damit in den nachfolgenden Methoden auf die grundlegenden Vektoroperatoren zurückgegriffen werden kann, müssen beide Koordinaten die gleiche Dimension besitzen.
- Mindestens einen Konstruktor, der zwei Koordinaten entgegennimmt.
- Eine Methode, die einen Punkt x(λ) auf der Geraden g bestimmt.
- Eine Methode, die den Abstand d eines Punktes x von der Geraden g berechnet.
- Eine Methode, die den Lotfußpunkt y eines Punktes x auf der Geraden g ermittelt (Projektionspunkt).
- Eine Methode, die den Schnittpunkt s von zwei Geraden g1 und g2 berechnet.
Anmerkung:
Da Geraden aus dem Undlichen kommen und ins Unendliche führen, gibt es kein geometrisches Kriterium. Programmiertechnisch besteht aber ein kleinster Wert für das Ergebnis des Kreuzproduktes, der nicht unterschritten werden darf: Double.MIN_VALUE (= 2-1074).
Aufgabe 7:
Ergänzend zur Klasse Line sollten in LinSeg folgende Methoden zur Verfügung stehen:
- Berechnung der Streckenlänge
- Prüfung: Ist die Streckenlänge größer als ε (im Konstruktor) ?
- Prüfung: Ist der Abstand des Punktes von der Strecke s (Geraden) größer als ε ?
- Prüfung: Liegt der Punkt x bzw. sein Lotfußpunkt noch auf der Strecke?
- Berechnung des Schnittpunktes der Strecken s1 und s2
- Prüfung: Schneiden oder berühren sich die Strecken s1 und s2 ?
- Prüfung: Verlaufen die beiden Strecken s1 und s2 parallel ?
Anmerkung:
Anders als Geraden sind Strecken durch ihren Anfangs- und Endpunkt begrenzt.
Geometrisches Kriterium zur Prüfung der Parallelität:
Sind die Abstände des Anfangs- und Endpunktes von der anderen Strecke s2 kleiner als ε, oder unterscheiden sich die Abstände um weniger als ε, liegt Parallelität vor! (siehe Abbildung: Punkte liegen innerhalb des grauen ε-Bereichs)